1. Introduction
It is almost impossible to deduce the three-dimensional
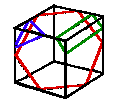
shape of an object from a thin section. One of the best examples
was provided by Smith (1956) and is shown in the following figure,
where some of the possible sections originating from a cube are
included (e.g. a triangle, a square, a rectangle, a hexagon).

You should also bear in mind that the section observed is tangential
or subtangential in many cases, which can lead to mistaken interpretations,
for example, the cross sections of channels may appear as oval
or spherical voids and will rarely appear elongated.

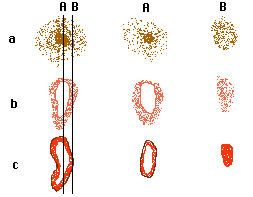
A tangential section (B) of a nucleic nodule (a) may not touch the nucleus and appear as a typical nodule: a subtangential section of a channel or a cavity or hypo- or quasi-coating (b) may simulate the presence of impregnative nodules (B). A tangential section of a coating of a channel (c) may appear as an infilling (B). The sections (A) would give correct interpretations.
Neither is it probable that the grains are cut according to their longest diameter (figure of the cube), so in the thin section, they will generally appear smaller than their real size.
Only the section that appears as a result of cutting the grain through its central part shows the real diameter.
For the same reason, you hardly ever see skeleton
grains in contact with others on thin sections, since the point
of contact is located outside the plane of the cut section in
the majority of the cases. A closed coarse sand grain packing
will appear on the thin section as a cluster of isolated grains
that are at a certain distance from each other.